| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 비모수적 모델
- deep learning #segmentation #sementic #pytorch #UNETR #transformer #UNET #3D #3D medical image
- 모수적 모델
- nlp
- 확산강조영상
- parrec
- non-parametric model
- words encoding
- 확산텐서영상
- decorater
- 데코레이터
- 코드오류
- paper review
- MICCAI
- parametric model
- 유전역학
- parer review
- monai
- nfiti
- TeCNO
- Surgical video analysis
- precision #정밀도 #민감도 #sensitivity #특이도 #specifisity #F1 score #dice score #confusion matrix #recall #PR-AUC #ROC-AUC #PR curve #ROC curve #NPV #PPV
- PYTHON
- Phase recognition
- nibabel
- TabNet
- tabular
- MRI
- genetic epidemiology
- 파이썬
- Today
- Total
KimbgAI
FLOPs란? 딥러닝 연산량에 대해서.. 본문
논문들을 보고있노라면 FLOPs라는 개념이 등장하는데, 대충 연산량? 모델의 크기? 등 추상적으로 알고 있던 내용이라 정확한 개념을 알아보고자 정리를 해보았다.

찾아보니 연산량에 대한 다양한 개념을 접할 수 있었다.
FLOPs? FLOPS? MAC? 등..
정리해보자
FLOPs(FLoating point OPerations)는 부동소수점 연산을 의미합니다.
FLOPs에서의 연산은 사칙연산을 포함하여 root, log, exponential 등의 연산도 해당되며, 각각을 1회 연산으로 계산합니다.
반면, FLOPS는 FLoating point Operations Per Second의 약자로, 1초당 얼마나 많은 연산을 처리할 수 있느냐하는 하드웨어의 퍼포먼스 측면을 본다는 점에서 차이가 있습니다.

MAC(Multiply–ACcumulate)
대부분의 현대 하드웨어는 tensor를 다루는 연산을 할때 FMA라고 하는 명령어 셋을 사용한다고 하는데,
이 FMA는 a*x+b를 하나의 연산(operation)으로 처리를 하고 이 연산이 몇번 실행되었는지를 세는 것이 MAC이다.
따라서 2 FLOPs는 1 MAC에 해당한다.
그렇다면 딥러닝 연산에 해당 FLOPs를 한번 계산해봅시다.
(내적, Fully connected layer, Convolution, Activation function 등)
내적(Dot product)
y = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + ... + w[n-1]*x[n-1]길이가 n인 두 벡터 x, y의 FLOPs는 2n-1입니다.
(곱하기가 n번, 더하기가 n-1번)
Fully connected layer
Fully connected layer 연산은 모든 인풋과 아웃풋이 완전히 연결되어있습니다.
인풋이 n개, 아웃풋이 m개라면, 아웃풋 m개에 대한 내적 n번 일어나기 때문에 (2n-1)*m FLOPs가 됩니다.
Convolution 연산
Convolution 연산의 인풋은 H(높이) x W(너비) x C(채널)의 3차원 텐서입니다.
kernel size가 K x K 라고 하면, FLOPs는 K∗K∗Cin∗Cout∗Hout∗Wout 이 됩니다. (대략적인 FLOPs.. 더하기는 전체 multiplcation 연산에 비해 현저히 적기 때문에 보통 생략한다고 합니다)

인풋이 아니라 아웃풋으로 계산되는 이유는 stride, padding 등을 적용한 결과가 out shape이기 때문입니다.
Activation function
ReLU는 y = max(0, x) 이므로 x의 길이가 n 이라면 FLOPs는 n
Sigmoid는 y = 1/(1+exp(-x)) 이므로 나누기, 더하기, -1 곱하기, exponential 연산으로 FLOPs는 4n
하지만 보통 딥러닝 모델의 전체 FLOPs에서는 차지하는 양이 미미하기때문에 생략한다고 합니다.
이처럼 Convolution과 FCL의 연산량이 상당하기 때문에, 많은 딥러닝 모델들이 이런 연산을 줄이고자 노력했습니다.
대표적인 방법론이 Depthwise seperable convolution 입니다.
인풋 x∈(Cin,Hin,Win) 가 있을때 1개의 feature map을 만들기 위해 standard convolution의 연산량은 위에서 계산했던 것과 같이 K∗K∗Cin∗Cout∗Hout∗Wout 입니다.
하지만 Depthwise seperable convolution 은 1개의 feature map을 얻기 위해서 depthwise convolution 과 pointwise convolution 으로 나누어 진다.
depthwise convolution 은 인풋의 채널을 나누어 각각 계산한다.
FLOPs는 K∗K∗Cout∗Hout∗Wout 입니다.

pointwise convolution은 1x1 필터를 가진 convolution이라고 생각하면 되고,
FLOPs는 1∗1∗Cout∗Hout∗Wout 이다.
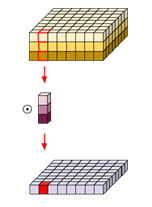
즉, 결과적으로 Depthwise seperable convolution 의 FLOPs는
(K∗K∗Cout∗Hout∗Wout)+(1∗1∗Cout∗Hout∗Wout) 으로
(K∗K+1)∗Cout∗Hout∗Wout 이다.
일반적인 Convolution의 1/Cin배 줄어드는 효과가 있다.
끝!
출처
https://bongjasee.tistory.com/3
https://hongl.tistory.com/31#recentEntries
'machine learning' 카테고리의 다른 글
| [ML] Dice loss & Dice Score with monai, pytorch (0) | 2022.11.08 |
|---|---|
| [ML][pytorch] torch.nn 과 torch.nn.Functional 의 차이 (0) | 2022.11.08 |
| [ML] VNet(16.06) 요약 및 코드 구현 (pytorch) (0) | 2022.11.01 |
| Brain MRI의 자동화된 segmentation을 위한 CAT12 사용법(CAT, Brainstorm, SPM) (0) | 2022.10.19 |
| [ML] U-Net(2015.05); Convolutional Networks for Biomedical Image Segmentation 요약 및 pytorch 코드 구현(2) (0) | 2022.10.13 |



